|
Test of Time Award
|
This paper introduces a stochastic variational gradient based inference procedure for training Latent Dirichlet Allocation (LDA) models on very large text corpora. On the theoretical side it is shown that the training procedure converges to a local optimum and that, surprisingly, the simple stochastic gradient updates correspond to a stochastic natural gradient of the evidence lower bound (ELBO) objective. On the empirical side the authors show that for the first time LDA can be comfortably trained on text corpora of several hundreds of thousands of documents, making it a practical technique for “big data” problems. The idea has made a large impact in the ML community because it represented the first stepping stone for general stochastic gradient variational inference procedures for a much broader class of models. After this paper, there would be no good reason to ever use full batch training procedures for variational inference anymore. |
|
Outstanding Paper
|
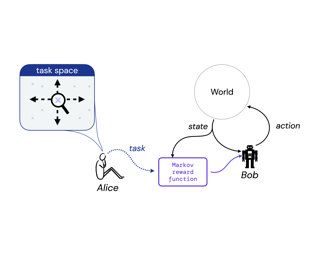
Reward is the driving force for reinforcement-learning agents. This paper is dedicated to understanding the expressivity of reward as a way to capture tasks that we would want an agent to perform. We frame this study around three new abstract notions of “task” that might be desirable: (1) a set of acceptable behaviors, (2) a partial ordering over behaviors, or (3) a partial ordering over trajectories. Our main results prove that while reward can express many of these tasks, there exist instances of each task type that no Markov reward function can capture. We then provide a set of polynomial-time algorithms that construct a Markov reward function that allows an agent to optimize tasks of each of these three types, and correctly determine when no such reward function exists. We conclude with an empirical study that corroborates and illustrates our theoretical findings. |
|
Outstanding Paper
|

We introduce the ``continuized'' Nesterov acceleration, a close variant of Nesterov acceleration whose variables are indexed by a continuous time parameter. The two variables continuously mix following a linear ordinary differential equation and take gradient steps at random times. This continuized variant benefits from the best of the continuous and the discrete frameworks: as a continuous process, one can use differential calculus to analyze convergence and obtain analytical expressions for the parameters; but a discretization of the continuized process can be computed exactly with convergence rates similar to those of Nesterov original acceleration. We show that the discretization has the same structure as Nesterov acceleration, but with random parameters. We provide continuized Nesterov acceleration under deterministic as well as stochastic gradients, with either additive or multiplicative noise. Finally, using our continuized framework and expressing the gossip averaging problem as the stochastic minimization of a certain energy function, we provide the first rigorous acceleration of asynchronous gossip algorithms. |
|
Outstanding Paper
|
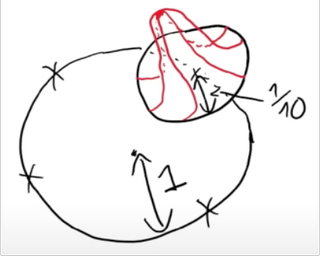
Classically, data interpolation with a parametrized model class is possible as long as the number of parameters is larger than the number of equations to be satisfied. A puzzling phenomenon in the current practice of deep learning is that models are trained with many more parameters than what this classical theory would suggest. We propose a theoretical explanation for this phenomenon. We prove that for a broad class of data distributions and model classes, overparametrization is {\em necessary} if one wants to interpolate the data {\em smoothly}. Namely we show that {\em smooth} interpolation requires $d$ times more parameters than mere interpolation, where $d$ is the ambient data dimension. We prove this universal law of robustness for any smoothly parametrized function class with polynomial size weights, and any covariate distribution verifying isoperimetry. In the case of two-layers neural networks and Gaussian covariates, this law was conjectured in prior work by Bubeck, Li and Nagaraj. We also give an interpretation of our result as an improved generalization bound for model classes consisting of smooth functions.
|
|
Outstanding Paper
|

Deep reinforcement learning (RL) algorithms are predominantly evaluated by comparing their relative performance on a large suite of tasks. Most published results on deep RL benchmarks compare point estimates of aggregate performance such as mean and median scores across tasks, ignoring the statistical uncertainty implied by the use of a finite number of training runs. Beginning with the Arcade Learning Environment (ALE), the shift towards computationally-demanding benchmarks has led to the practice of evaluating only a small number of runs per task, exacerbating the statistical uncertainty in point estimates. In this paper, we argue that reliable evaluation in the few run deep RL regime cannot ignore the uncertainty in results without running the risk of slowing down progress in the field. We illustrate this point using a case study on the Atari 100k benchmark, where we find substantial discrepancies between conclusions drawn from point estimates alone versus a more thorough statistical analysis. With the aim of increasing the field's confidence in reported results with a handful of runs, we advocate for reporting interval estimates of aggregate performance and propose performance profiles to account for the variability in results, as well as present more robust and efficient aggregate metrics, such as … |
|
Outstanding Paper
|

We introduce the ``continuized'' Nesterov acceleration, a close variant of Nesterov acceleration whose variables are indexed by a continuous time parameter. The two variables continuously mix following a linear ordinary differential equation and take gradient steps at random times. This continuized variant benefits from the best of the continuous and the discrete frameworks: as a continuous process, one can use differential calculus to analyze convergence and obtain analytical expressions for the parameters; but a discretization of the continuized process can be computed exactly with convergence rates similar to those of Nesterov original acceleration. We show that the discretization has the same structure as Nesterov acceleration, but with random parameters. We provide continuized Nesterov acceleration under deterministic as well as stochastic gradients, with either additive or multiplicative noise. Finally, using our continuized framework and expressing the gossip averaging problem as the stochastic minimization of a certain energy function, we provide the first rigorous acceleration of asynchronous gossip algorithms. |
|
Outstanding Paper
|

We are interested in learning generative models for complex geometries described via manifolds, such as spheres, tori, and other implicit surfaces. Current extensions of existing (Euclidean) generative models are restricted to specific geometries and typically suffer from high computational costs. We introduce Moser Flow (MF), a new class of generative models within the family of continuous normalizing flows (CNF). MF also produces a CNF via a solution to the change-of-variable formula, however differently from other CNF methods, its model (learned) density is parameterized as the source (prior) density minus the divergence of a neural network (NN). The divergence is a local, linear differential operator, easy to approximate and calculate on manifolds. Therefore, unlike other CNFs, MF does not require invoking or backpropagating through an ODE solver during training. Furthermore, representing the model density explicitly as the divergence of a NN rather than as a solution of an ODE facilitates learning high fidelity densities. Theoretically, we prove that MF constitutes a universal density approximator under suitable assumptions. Empirically, we demonstrate for the first time the use of flow models for sampling from general curved surfaces and achieve significant improvements in density estimation, sample quality, and training complexity over existing CNFs on … |
|
Outstanding Paper
|

We are interested in learning generative models for complex geometries described via manifolds, such as spheres, tori, and other implicit surfaces. Current extensions of existing (Euclidean) generative models are restricted to specific geometries and typically suffer from high computational costs. We introduce Moser Flow (MF), a new class of generative models within the family of continuous normalizing flows (CNF). MF also produces a CNF via a solution to the change-of-variable formula, however differently from other CNF methods, its model (learned) density is parameterized as the source (prior) density minus the divergence of a neural network (NN). The divergence is a local, linear differential operator, easy to approximate and calculate on manifolds. Therefore, unlike other CNFs, MF does not require invoking or backpropagating through an ODE solver during training. Furthermore, representing the model density explicitly as the divergence of a NN rather than as a solution of an ODE facilitates learning high fidelity densities. Theoretically, we prove that MF constitutes a universal density approximator under suitable assumptions. Empirically, we demonstrate for the first time the use of flow models for sampling from general curved surfaces and achieve significant improvements in density estimation, sample quality, and training complexity over existing CNFs on … |
|
Outstanding Paper
|
[ Virtual ] 
Deep reinforcement learning (RL) algorithms are predominantly evaluated by comparing their relative performance on a large suite of tasks. Most published results on deep RL benchmarks compare point estimates of aggregate performance such as mean and median scores across tasks, ignoring the statistical uncertainty implied by the use of a finite number of training runs. Beginning with the Arcade Learning Environment (ALE), the shift towards computationally-demanding benchmarks has led to the practice of evaluating only a small number of runs per task, exacerbating the statistical uncertainty in point estimates. In this paper, we argue that reliable evaluation in the few run deep RL regime cannot ignore the uncertainty in results without running the risk of slowing down progress in the field. We illustrate this point using a case study on the Atari 100k benchmark, where we find substantial discrepancies between conclusions drawn from point estimates alone versus a more thorough statistical analysis. With the aim of increasing the field's confidence in reported results with a handful of runs, we advocate for reporting interval estimates of aggregate performance and propose performance profiles to account for the variability in results, as well as present more robust and efficient aggregate metrics, such as … |
|
Outstanding Paper
|
[ Virtual ] 
Classically, data interpolation with a parametrized model class is possible as long as the number of parameters is larger than the number of equations to be satisfied. A puzzling phenomenon in the current practice of deep learning is that models are trained with many more parameters than what this classical theory would suggest. We propose a theoretical explanation for this phenomenon. We prove that for a broad class of data distributions and model classes, overparametrization is {\em necessary} if one wants to interpolate the data {\em smoothly}. Namely we show that {\em smooth} interpolation requires $d$ times more parameters than mere interpolation, where $d$ is the ambient data dimension. We prove this universal law of robustness for any smoothly parametrized function class with polynomial size weights, and any covariate distribution verifying isoperimetry. In the case of two-layers neural networks and Gaussian covariates, this law was conjectured in prior work by Bubeck, Li and Nagaraj. We also give an interpretation of our result as an improved generalization bound for model classes consisting of smooth functions.
|
|
Outstanding Paper
|
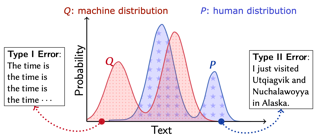
As major progress is made in open-ended text generation, measuring how close machine-generated text is to human language remains a critical open problem. We introduce Mauve, a comparison measure for open-ended text generation, which directly compares the learnt distribution from a text generation model to the distribution of human-written text using divergence frontiers. Mauve scales up to modern text generation models by computing information divergences in a quantized embedding space. Through an extensive empirical study on three open-ended generation tasks, we find that Mauve identifies known properties of generated text, scales naturally with model size, and correlates with human judgments, with fewer restrictions than existing distributional evaluation metrics. |
|
Outstanding Paper
|

As major progress is made in open-ended text generation, measuring how close machine-generated text is to human language remains a critical open problem. We introduce Mauve, a comparison measure for open-ended text generation, which directly compares the learnt distribution from a text generation model to the distribution of human-written text using divergence frontiers. Mauve scales up to modern text generation models by computing information divergences in a quantized embedding space. Through an extensive empirical study on three open-ended generation tasks, we find that Mauve identifies known properties of generated text, scales naturally with model size, and correlates with human judgments, with fewer restrictions than existing distributional evaluation metrics. |
|
Outstanding Paper
|

Reward is the driving force for reinforcement-learning agents. This paper is dedicated to understanding the expressivity of reward as a way to capture tasks that we would want an agent to perform. We frame this study around three new abstract notions of “task” that might be desirable: (1) a set of acceptable behaviors, (2) a partial ordering over behaviors, or (3) a partial ordering over trajectories. Our main results prove that while reward can express many of these tasks, there exist instances of each task type that no Markov reward function can capture. We then provide a set of polynomial-time algorithms that construct a Markov reward function that allows an agent to optimize tasks of each of these three types, and correctly determine when no such reward function exists. We conclude with an empirical study that corroborates and illustrates our theoretical findings. |
|
Datasets and Benchmarks Award
|
Benchmark datasets play a central role in the organization of machine learning research. They coordinate researchers around shared research problems and serve as a measure of progress towards shared goals. Despite the foundational role of benchmarking practices in this field, relatively little attention has been paid to the dynamics of benchmark dataset use and reuse, within or across machine learning subcommunities. In this paper, we dig into these dynamics. We study how dataset usage patterns differ across machine learning subcommunities and across time from 2015-2020. We find increasing concentration on fewer and fewer datasets within task communities, significant adoption of datasets from other tasks, and concentration across the field on datasets that have been introduced by researchers situated within a small number of elite institutions. Our results have implications for scientific evaluation, AI ethics, and equity/access within the field. |
|
Datasets and Benchmarks Award
|
Computational methods that operate on three-dimensional (3D) molecular structure have the potential to solve important problems in biology and chemistry. Deep neural networks have gained significant attention, but their widespread adoption in the biomolecular domain has been limited by a lack of either systematic performance benchmarks or a unified toolkit for interacting with 3D molecular data. To address this, we present ATOM3D, a collection of both novel and existing benchmark datasets spanning several key classes of biomolecules. We implement several types of 3D molecular learning methods for each of these tasks and show that they consistently improve performance relative to methods based on one- and two-dimensional representations. The choice of architecture proves to be important for performance, with 3D convolutional networks excelling at tasks involving complex geometries, graph networks performing well on systems requiring detailed positional information, and the more recently developed equivariant networks showing significant promise. Our results indicate that many molecular problems stand to gain from 3D molecular learning, and that there is potential for substantial further improvement on many tasks. To lower the barrier to entry and facilitate further developments in the field, we also provide a comprehensive suite of tools for dataset processing, model training, and … |